560. Subarray Sum Equals K

Given an array of integers and an integer k, you need to find the total number of continuous subarrays whose sum equals to k.

Example 1:
Input:nums = [1,1,1], k = 2
Output: 2
Note:

1. The length of the array is in range [1, 20,000].
2. The range of numbers in the array is [-1000, 1000] and the range of the integer k is [-1e7, 1e7].

找出一个数组中连续元素之和为k的组合个数。

1. Brute Force 剪枝

求出每一个元素与后面元素之和的最大最小值，当一个元素与后一个元素的最小值之和大于k或者与后一个元素的最大值之和小于k就可以断定后面不存在满足条件的集合，可以直接跳过。

class Solution {
    public int subarraySum(int[] nums, int k) {
        if (nums == null) return 0;
        int r = 0;
        int[] min = new int[nums.length];
        int[] max = new int[nums.length];
        min[nums.length - 1] = nums[nums.length - 1];
        max[nums.length - 1] = nums[nums.length - 1];
        for (int i = nums.length - 2; i >= 0; i--) {
            min[i] = Math.min(min[i + 1] + nums[i], nums[i]);
            max[i] = Math.max(max[i + 1] + nums[i], nums[i]);
        }
        for (int i = 0; i < nums.length ; i++) {
            int cur = nums[i];
            if (cur == k) r++;
            for (int j = i + 1; j < nums.length; j++) {
                if (cur + nums[j] == k) r++;
                if (cur + min[j] > k || cur + max[j] < k) break;
                cur += nums[j];
            }
        }
        return r;
    }
}

时间复杂度为O(m * n)，空间复杂度为O(n)

2. DP

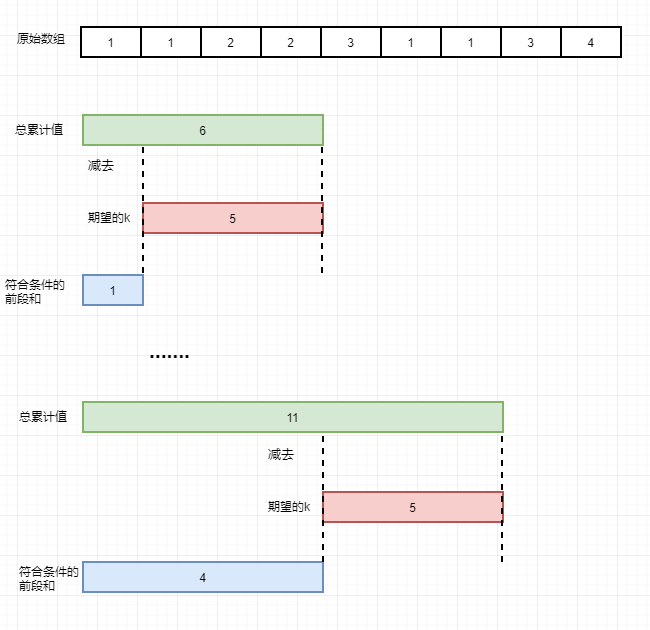
将每次累加的结果保存起来，而其中任意一段的累加和可以通过两段累加和相减得到

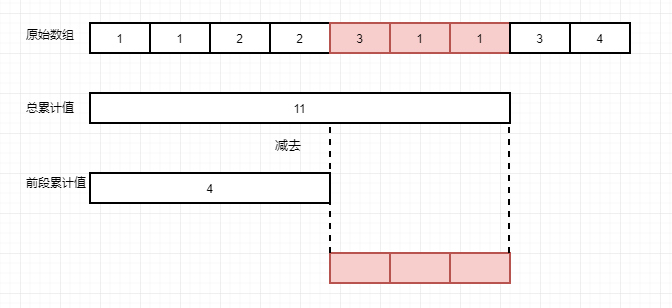
利用上述思想可以：

• 遍历整个数组，把累加和计算一遍并保存起来
• 累加和减去我们期望的k值，如果结果在之前的累加结果中存在则可判定为符合条件。

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0, sum = 0;
        Map<Integer, Integer> map = new HashMap<>(nums.length);
        map.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            if (map.containsKey(sum - k)) count += map.get(sum - k);
            map.put(sum, map.getOrDefault(sum, 0) + 1);
        }
        return count;
    }
}

时间复杂度为O(n)，空间复杂度为O(n)